WHY DOES A BICYCLE KEEP UPRIGHT?
By F. G. Maunsell.
1. General Considerations.
Most of us have asked this question at some time or another; generally we have received some such answer as: “It's a gyroscopic effect, of course”. Further details are not easy to obtain, and the majority of books on Mechanics do not mention the subject.
I have, however, found some references, which seem to be of sufficient interest to be quoted. They are as follows:
(i) The “Encyclopaedia Britannica”. The thirteenth edition has nothing of import in the articles on “Bicycle” and “Cycling” : the fourteenth edition (under “Bicycle”) has the following sentence, which does not, indeed purport to answer the question of uprightness, but which is, perhaps, of some interest: “The slope or steering angle is the cause of a bicycle remaining naturally in a straight line, because any movement of the wheel out of the straight tends to raise the bicycle slightly: therefore the weight of the bicycle and rider discourages any such deflection of the front wheel . . .”. I may add that nothing before or after helps to elucidate this remarkable theory.
(ii) A. Gray : “A Treatise on Gyrostatics and Rotational Motion”, 1918. In Chap. VII, para. 12, appears the following explanation: “If the rider feels himself beginning to fall over to one side or the other he instinctively turns the bicycle towards that side, and the inertia in the forward movement, assisted by the gyrostatic action of the driving wheel, over which the rider sits, causes the bicycle frame to set itself erect again”.
(iii) R. W. Pohl : “Physical Principles of Mechanics and Acoustics”, English translation, 1932. Chap. VII, para. 11, gives the following explanation, headed “Riding a bicycle without touching the handlebars” : “Suppose the rider tilts a little towards the right ... the front wheel, acting as a gyrostat, describes a, precessional motion about the vertical and curves to the right. The line joining the points of contact of the front and back wheels with the ground is again brought under the centre of gravity of the rider, that is, the point of support is brought back under the centre of gravity.”
(iv) Appell : Mécanique Rationnelle, II, has a section on bicycles (para. 422). He apparently holds the view that the cyclist deliberately turns the handlebars towards the side to which he is falling. This turning of the handlebars brings the bicycle upright again by means of centrifugal action. Appell gives references to four papers on the bicycle and to a book by Bouriet – ‘Nouveau traité des bicycles et bicyclettes’. I have not been able to consult this book, but it is referred to in Bourlet's paper mentioned below and apparently contains no more new theories.
The four papers are as follows:
(v) Bourlet: Bull. Soc. Math., 1899.
(vi) Boussinesq: Jordan’s Journal de Math., 1899.
(vii) Routh: Mess. of Math., 1898-9.
(viii) Carvallo: Journ. de l’École Poly. (V, VI, 1900).
Al1 four writers take, broadly speaking, the same views as Appell. Carvallo alone goes somewhat further and considers the case of riding without touching the handlebars. He alone appears to appreciate the construction of the front fork which, as I shall explain later, ensures that turning the handlebars lowers the centre of gravity. Unfortunately (from my point of view, at any rate) Carvallo treats the problem entirely analytically, and I have not yet had time to follow out in full the long and involved calculations of his paper (which runs to more than l00 pages). I hope to do so in the near future.
He reaches the remarkable result that a, bicycle ridden without touching the handlebars is stable for a band of velocities. That is, it is unstable for velocities both very 1ow and very high. However, the mechanism of this result is not clear.
(ix) The Editor of Cycling informs me that the matter was put before the Brains Trust in December 1942, and their reply was printed in Cycling in their issue of January 6,1943. Unfortunately he could not supply me with a copy of this article, and I should be very much obliged if anyone who happens to possess a copy could lend it to me for a short period.
(x) The Editor of Cycling also sent me the views of his technical expert. The views he puts forward are that the principal cause of a bicycle remaining upright is the deliberate balancing by the rider moving the handlebars from side to side, thus moving the point of support under the centre of gravity of the machine and rider. He also states that a fixed-wheel machine can be balanced at very slow speeds and even when stationary, although a free-wheel one cannot. Accepting this as an experimental fact, I confess I cannot see the reason for it.
Even these few quotations show that there exists a certain confusion of ideas on the subject, and I will now attempt to classify the theories that I have heard put forward to explain the effect. All but one of these connect (correctly, I believe) the restoration of uprightness with the turning of the handlebars towards the side to which the bicycle is falling. The exception is :
Theory A. This asserts simply that a tendency to fall to the right is counter-acted by the rider shifting his weight to the left. This action is certainly not a conscious one, and is presumably a subconscious reaction acquired when learning to ride. The theory is, however, certainly incorrect. If it were true, it would be as easy to balance a bicycle on which the handlebars were rigidly prevented from turning or a stationary bicycle as a bicycle ridden in the ordinary way. On the contrary, these two feats are extremely difficult to accomplish, if not impossible.
All the other theories agree that when the bicycle starts to fall to the right, the handlebars are turned to the right, and that this action causes the bicycle to regain the upright position. There are therefore two questions to be answered. Firstly, “Why do the handlebars turn to the right when the bicycle starts to fall to the right?” Secondly, “Why does turning the handlebars to the right when the bicycle starts to fall to the right have the effect of causing the bicycle to regain the upright position?”
The theories put forward to account for the first effect are as follows :
Theory B1. This is the theory, as put forward by Gray in the second of the above quotations, that the turn is due to the instinctive (subconscious is perhaps a better word) action of the rider. The simplest answer to this is the fact that it is possible to ride a bicycle without holding the handlebars.
Theory B2. The theory, given by Pohl, that the turning of the handlebars is due to the gyrostatic precession of the front wheel. That this effect exists is undoubted. Later in this paper I hope to show that it is of secondary importance compared to a further effect.
Theory B3. This further effect I have called the “statical” effect. It depends on the fact that when the bicycle is tilted slightly to the right, a slight turn of the handlebars to the right lowers the centre of gravity, while a slight turn to the left raises it. The effect is present whether the bicycle is moving or stationary and can be tested immediately by anyone with his own bicycle in the latter case.
So much for why the handlebars are turned. Now for theories why this turning causes the bicycle to come upright again.
Theory C1. Gray’s theory that it is due to gyrostatic action on the back wheel (“driving wheel” presumably means this). Some such action there will be: I shall show that it is much too small quantitatively.
Theory C2. Pohl’s theory that the turning of the handlebars shifts the line joining the points of contact of the front and back wheels with the ground sounds plausible. Unfortunately, it is in direct conflict with the facts. The line of the front head, i.e. the axis about which the front wheel turns when the handlebars are turned, meets the ground about three inches in front of the point of contact of the front wheel when the bicycle is upright. Consequently, for small deflections of the front wheel to the right, the point of contact of the front wheel goes to the left, and the bicycle is, due to this cause, more and not less inclined to fall to the right. It is true that a large deflection to the right will send the point of contact to the right, due to the forward bend in the front forks. This is why, if you try to balance on a stationary bicycle, a tendency to a fall to the right can be stopped by a violent right-hand turn to the handlebars. We are, however, conceded only with small deflections in the problem of the moving bicycle.
Theory C3. The completely satisfactory explanation of this part of the effect is that it is due to “centrifugal force”. In other words, turning the handlebars to the right makes the bicycle describe a curve to the right. Thus the bicycle is given an acceleration normal to the curve, that is, to the right. The only forces that can produce this acceleration are sideways reactions on the points of contact of the wheels with the ground, and these reactions, directed to the right, have a, moment about the centre of gravity which forces the machine to rise again to the upright position.
To sum up, the explanation I put forward as the correct one is compounded of theories B3 and C3. When the bicycle starts to fall to the right, the “statical” effect causes the handlebars to turn to the right and the “centrifugal” effect causes the bicycle to return to the upright position. The function of the rider's hands is simply to act as a steadying agent and prevent a too violent oscillation occurring.
It is agreed that the gyrostatic effects B2 and C1 tend to act in the same way. In order to decide between B2 and B3 and between C1 and C3 a quantitative investigation is necessary.
2. Quantitative Work.
As we only require to get an idea of the relative orders of magnitude of the effects, quite rough estimates of the various weights and lengths involved will be sufficient for our purpose. In what follows I have obtained some of the data by rough measurements of my own bicycle, others by estimation.
m = mass of front wheel = 4.25 1b.
r = radius of front wheel = 1.1 ft.
k = radius of gyration of front wheel about its axle = 0.4 ft.
M = mass of bicycle plus rider = l75 lb.
a = height of c.g. of bicycle plus rider = 3.5 ft.
b = distance between back and front axles = 3.5 ft.
λ = ratio of weight on back to weight on front wheel = 4.
α = rake of front head from vertical = 30.0°.
d = distance in front of point of contact with ground that prolongation
of front head meets ground = 3 in. = 0.25 ft.
v = velocity of bicycle, say, 10 ft./sec.
ψ = sideways tilt of the bicycle.
From the above are derived:
n = angular velocity of front wheel = 9.1 radians/sec.
C = moment of inertia of front wheel about its axle = 0.7 lb.-ft.2
The gyroscopic effect B2.
When the bicycle starts to fall sideways, we require the angular velocity ψdot about a horizontal axis. This, of course, increases from zero as ψ increases from zero. Taking the mass as concentrated at the c.g., by the ordinary formula:
½ * l75 * 3.52 * ψdot2 = 3.5 * 32 * 3.5 * (1 - cos ψ).
This gives for ψ = 1°, ψdot = 0.05 radians/sec.
ψ = 5°, ψdot = 0.26 radians/sec.
Now the couple L1 acting on the front wheel and tending to turn it to the right = C n ψdot = 0.7 * 9.1 * ψdot.
Hence for ψ = 1°, L1 = 0.3 pdls.-ft.
ψ = 5°, L1 = 1.7 pdls.-ft.
This couple L1 is about a vertical line : the resolved part about the axis formed by the front head is L1*cos 30°, or 0.25, l.5 pdls.-ft. respectively.
The statical effect B3.
We suppose the bicycle has tilted an angle ψ to the right, and we require the couple due to the weight which tends to turn the front wheel to the right. To find this we suppose the handlebars turned a small angle β, and we work out how far the centre of gravity sinks.

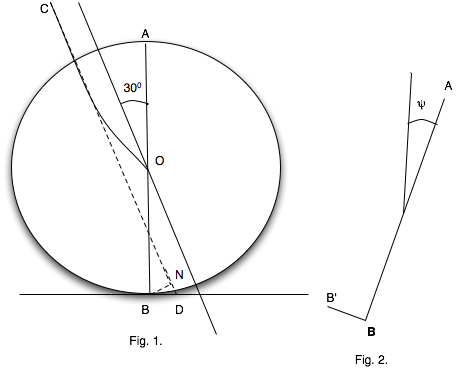
Fig. 1 represents the side elevation of the front wheel when the bicycle is upright. AOB is the vertical diameter. CND represents the line of the front head. BN is perpendicular to CD and BN=BD cos 30° = 0.25 cos 30° = 0.21 ft.
Fig. 2 represents the rear elevation of the front wheel when the bicycle is tilted at an angle ψ to the right.
When the front wheel is turned an angle β to the right, B describes (to the first order) a circle about N. So B moves to the neighbouring point B' where BB' = BN * α = 0.21 α ft.
Hence O sinks a distance BB' sin ψ = 0.21 * sin ψ.
The c.g. of the above machine will therefore sink one-fifth of this distance, that is, 0.04 α sin ψ
Hence the work done by gravity = 175 * 32 * 0.04 α sin ψ ft.-pdls.
The work done against the couple L2 which is required to keep the front wheel from turning to the right is L2α, and this must be equal to the former expression.
That is, L2 = l75 * 32 * 0.04 sin ψ.
If ψ = 1°, L2 = 4 pdls.-ft.
ψ = 5°, L2 = 20 pdls.-ft.
It will be seen that the “statical” effect C3 is nearly 10 times as great as the gyroscopic effect C2 even for the comparatively large tilt of 5°, and is proportionately more for smaller tilts. It is undoubtedly the major factor in causing the handlebars to turn in the direction of tilt.
The gyroscopic effect of C1.
Suppose the handlebars are turned an angle ψ. The bicycle will describe a circle to right whose radius ρ is given by the formula b/ρ = ψ (where ψ is in radians).
Thus when ψ = 1°, ρ = ( 3.5 * 180 )/ π ft.= 200 ft. ;
ψ = 5°, ρ = 40 ft.
Since we assume the velocity to be 10 ft./sec., the angular velocity ψdot with which this circle is described is
1/20, 1/4 rad./sec.
in the two cases.
The couple L3, which tends to right the bicycle due to the precessional action on one wheel, is C n ψdot.
The value of the couple L3 is, as in B2,
for ψ = 1° L3 = 0.3 pdls./ft.
ψ = 5°, L3 = 1.5 pdls./ft.
If we allow that both, wheels give a, precessional effect, we get
for ψ = 1° L3 = 0.6 pdls./ft.
ψ = 5°, L3 = 3.0 pdls-/ft.
The “centrifugal” effect C3.
As before, we consider the handlebars turned angles 1° or 5°.
The normal acceleration towards the right is then ψdot2 ρ, or 200/400, 40/16 respectively.
i.e. ½ ft./sec.2, 2½ ft./sec.2;
the righting couple is M * acceleration * height of centre of gravity, or
175 * 3.5 * acceleration.
This works out at 300, 1500 pdls.-ft. respectively, and it is clear that the effect C1 is insignificant compared to the effect C3.
F. G. Maunsell.
October 1946
Click here to go back to Salisbury Home Page